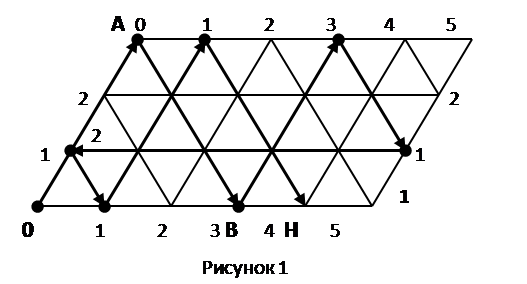
Всем известна игра бильярд за прямоугольным столом с лузами. Появившись до нашей эры в Индии и Китае, бильярд через много веков перекочевал в европейские страны – упоминание о нем имеется в английских летописях VI века. В России бильярд стал известен и распространился при Петре I. Подобно тому, как азартная игра в кости вызвала к жизни "исчисление" вероятностей, игра в бильярд послужила предметом серьезных научных исследований по механике и математике. Представьте себе горизонтальный бильярдный стол произвольной формы, но без луз. По этому столу без трения движется точечный шар, абсолютно упруго отражаясь от бортов стола. Спрашивается, какой может быть траектория этого шарика? Поиски ответа на этот вопрос и послужили появлению теории математического бильярда или теории траекторий.
Задачи на переливание жидкостей можно очень легко решать, вычерчивая бильярдную траекторию шара, отражающегося от бортов стола, имеющего форму параллелограмма.
Задача. Имеются два сосуда — трехлитровый и пятилитровый. Нужно, пользуясь этими сосудами, получить 1, 2, 3, 4, 5, 6, 7 и 8 литров воды. В нашем распоряжении водопроводный кран и раковина, куда можно выливать воду.
Решение. В рассматриваемой задаче стороны параллелограмма должны иметь длины 3 и 5 единиц. По горизонтали будем откладывать количество воды в литрах в 5-литровом сосуде, а по вертикали – в 3-литровом сосуде. На всем параллелограмме нанесена сетка из одинаковых равносторонних треугольников (см. рис.1)
Бильярдный шар может перемещаться только вдоль прямых, образующих сетку на параллелограмме. После удара о стороны параллелограмма шар отражается и продолжает движение вдоль выходящего из точки борта, где произошло соударение. При этом каждая точка параллелограмма, в которой происходит соударение, полностью характеризует, сколько воды находится в каждом из сосудов.
Пусть шар находится в левом нижнем углу и после удара начнет перемещаться вверх вдоль левой боковой стороны параллелограмма до тех пор, пока не достигнет верхней стороны в точке А. Это означает, что мы полностью наполнили водой малый сосуд. Отразившись упруго, шар покатится вправо вниз и ударится о нижний борт в точке В, координаты которой 3 по горизонтали и 0 по вертикали. Это означает, что в большом сосуде 3 литра воды, а в малом сосуде воды нет, то есть мы перелили воду из малого сосуда в большой сосуд.
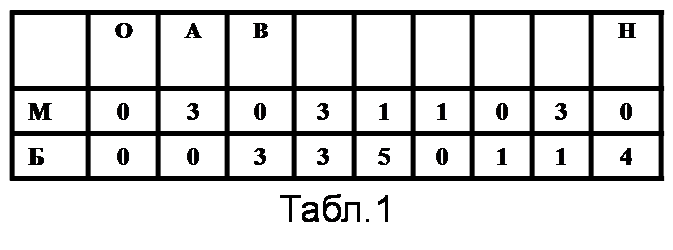
Прослеживая дальнейший путь шара и записывая все этапы его движения в виде отдельной таблицы (табл.1), в конце концов, мы попадаем в точку Н, которая соответствует состоянию, когда малый сосуд пуст, а в большом сосуде 4 литра воды. Таким образом, получен ответ и указана последовательность переливаний, позволяющих отмерить 4 литра воды. Все 8 переливаний изображены схематически в таблице.
Является ли это решение самым коротким? Нет, существует второй путь, когда воду сначала наливают в пятилитровый сосуд. Если на диаграмме шар из точки О покатится вправо по нижней стороне параллелограмма и затем, отразившись от правой боковой стороны, в точку 2 на верхней стороне параллелограмма и т.д., то получим более короткое решение задачи. Можно показать, что полученное решение с 6 переливаниями уже является самым коротким...
Источник: https://sites.google.com/site/resenielog/metod-matematiceskogo-bilarda
|